Updated 3 years ago
Minimum Edit Distance
The following interview was asked during a coding interview at Google:
Given two strings A and B, find the minimum number of steps required to convert A to B. (each operation is counted as 1 step.) You have the following 3 operations permitted on a word:
- Insert a character
- Delete a character
- Replace a character
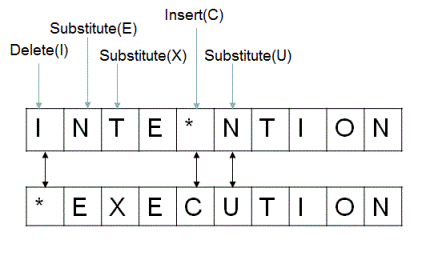
Here's a visual representation (source: iDeserve)
METHOD = '''
- if first char is equal just consider the problem with first chars ignored
- if the first char are not equal
- either it has to be deleted
- recursively solve by ignoring first char of first str
- or swapped
- recursively solve by ignoring first char of both str
- or a char must be inserted before it
- recursively solve by ignoring first char of second str
- Base would encountered when one of any string is empty
- We would simply return difference b/w length of remaining string and its current position
'''# Recursive Solution
def min_steps_1(a: str, b: str, idx_a=0, idx_b=0) -> int:
if idx_a == len(a):
return len(b) - idx_b
if idx_b == len(b):
return len(a) - idx_a
if a[idx_a] == b[idx_b]:
return min_steps_1(a, b, idx_a + 1, idx_b + 1)
deletion = min_steps_1(a, b, idx_a + 1, idx_b)
swapping = min_steps_1(a, b, idx_a + 1, idx_b + 1)
insertion = min_steps_1(a, b, idx_a, idx_b + 1)
return 1 + min(deletion, swapping, insertion)# Memoized Solution
def min_steps_2(a: str, b: str) -> int:
memo = {}
def recurse(idx_a=0, idx_b=0):
key = (idx_a, idx_b)
if key in memo:
return memo[key]
if idx_a == len(a):
memo[key] = len(b) - idx_b
elif idx_b == len(b):
memo[key] = len(a) - idx_a
elif a[idx_a] == b[idx_b]:
memo[key] = recurse(idx_a + 1, idx_b + 1)
else:
delete = recurse(idx_a + 1, idx_b)
swap = recurse(idx_a + 1, idx_b + 1)
insert = recurse(idx_a, idx_b + 1)
memo[key] = 1 + min(delete, swap, insert)
return memo[key]
return recurse()# Dynamic Solution
def min_steps_3(a: str, b: str) -> int:
m, n = len(a), len(b)
tab = [0] * max(m,n)
i = 0
while i < m and i < n:
if a[i] == b[i]:
tab[i] = tab[i-1]
else:
tab[i] = 1 + tab[i-1]
i += 1
while i < m or i < n:
tab[i] = 1 + tab[i-1]
i +=1
return tab