Jovian
Sign In
Learn practical skills, build real-world projects, and advance your career

Minimum Edit Distance

The following interview was asked during a coding interview at Google:

Given two strings A and B, find the minimum number of steps required to convert A to B. (each operation is counted as 1 step.) You have the following 3 operations permitted on a word:

  • Insert a character
  • Delete a character
  • Replace a character

Here's a visual representation (source: iDeserve)

alt

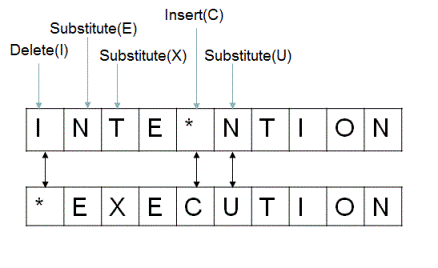
# Solve the problem here


# function signature
def min_step(str1, str2):
    pass


"""
recursion:
- if the first character is equal, then ignore from both
- if the first character is not equal,
    - either it has to be deleted
        - 1 + recursively solve after ignoring the first character of str1
    - or swapped
        - 1 + recursively solve after ignoring the first character of each
    - or a character inserted before
        - 1 + recursively solve after ignoring the first character of str2
"""
def min_step1(str1, str2, i1=0, i2=0):
    if i1 == len(str1):
        return len(str2) - i2
    elif i2 == len(str2):
        return len(str1) - i1
    elif str1[i1] == str2[i2]:
        return min_step1(str1, str2, i1+1, i2+1)
    else:
        return 1 + min(min_step1(str1, str2, i1+1, i2), # deletion
                       min_step1(str1, str2, i1+1, i2+1), # swap
                       min_step1(str1, str2, i1, i2+1)) # insertion



def min_step2(str1, str2):
    memo = {}
    def recurse(i1, i2):
        key = i1, i2
        if key in memo:
            return memo[key]
        elif i1 == len(str1):
            memo[key] = len(str2) - i2
        elif i2 == len(str2):
            memo[key] = len(str1) - i1
        elif str1[i1] == str2[i2]:
            memo[key] = recurse(i1+1, i2+1)
        else:
            memo[key] = 1 + min(recurse(i1+1, i2), 
                                recurse(i1+1, i2+1),
                                recurse(i1, i2+1))
        return memo[key]
    return recurse(0,0)
        
# Test the solution here

# input
str1 = "intention"
str2 = "execution"

# output
output1 = 5


"""
1. general case listed above
2. no change is required
3. all the characters need to be changed
4. equal length
5. unequal length
6. one of the string is empty
7. only deletion, only addition, only swapping
"""


min_step2(str1, str2)
5